犀牛建模实例图文教程,教你Rhino快速打造循环曲面“莫比乌斯”
犀牛建模之中曲面的建模无疑是比较难的,尤其是对于新人来说,犀牛建模里有几个比较经典的建模形态,也是广为流传的曲面建模方法,比如下面要为大家介绍的莫比乌斯曲面建模,网络上也有不少相关的建模思路和技巧的总结,为大家带来的这篇犀牛建模实例图文教程,教你Rhino快速打造循环曲面“莫比乌斯”,不失为一篇出色的曲面建模思路和方法的总结,推荐大家学习。
公元1858年,德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”。(也就是说,它的曲面只有一个)——百度百科
正如百度百科所说,莫比乌斯环的特别之处就在于它的“单面性”,很多无法在平面上解决的问题,也可以在莫比乌斯环上实现。莫比乌斯环的形体极具灵动性,在想要展示作品的曲面流动性时,很多同学们会将莫比乌斯环作为参考进行建模。

我们就以一个小摆饰为例,利用Rhino分解莫比乌斯的建模思维,帮助同学们更高效的完成相关形体的建模。
建立轮廓
首先确定苹果形状的轮廓线,用“控制点曲线”将形状的轮廓画出来。原则对称的物体可画一半就可以,另一半镜像,然后组合为一条封闭的曲线。
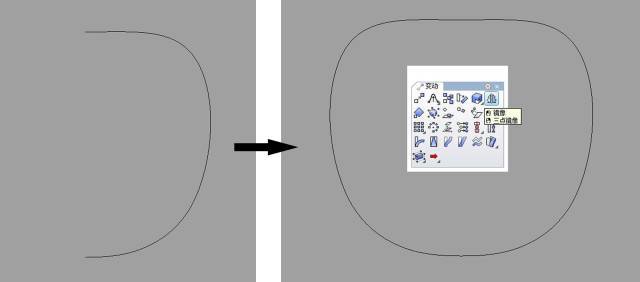
之后用“长度”命令把绘制好的长度分析出来备用,保证后面的操作物件不变形。
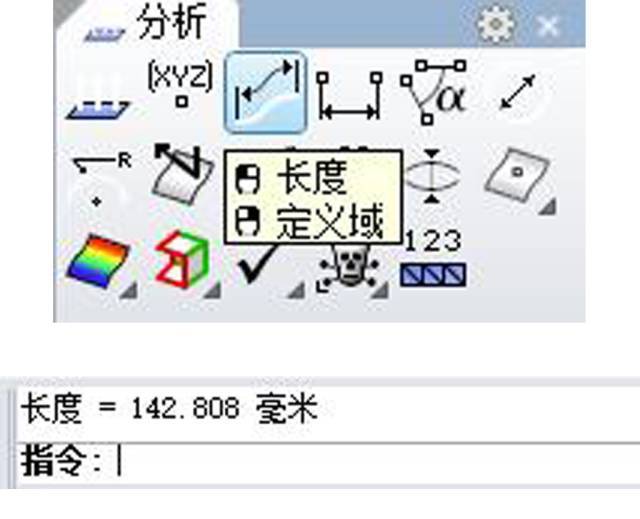
然后建立大形。这一部分先要绘制一个矩形,然后用“重建曲线”调整点数及控制点的位置,得到四边向内凹的形状。

捕捉矩形中心点,绘制一条垂直于矩形的直线,长度为第2步分析出的曲线长度。“直线挤出”将矩形挤出成曲面,同样挤出长度为第2步分析出的长度。若有小数可忽略,直接输出整数。
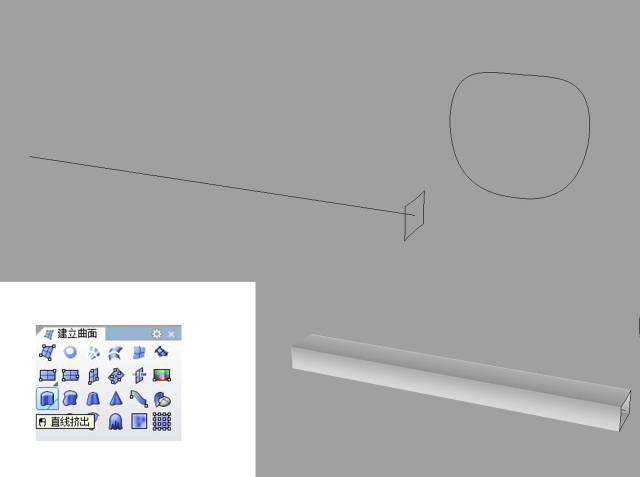
扭转曲面
整理曲线,“扭转”时,以上一步中绘制的直线为扭转轴,将挤出的曲面扭转180度,用“不等距边缘圆角”将四条边缘倒成圆角。
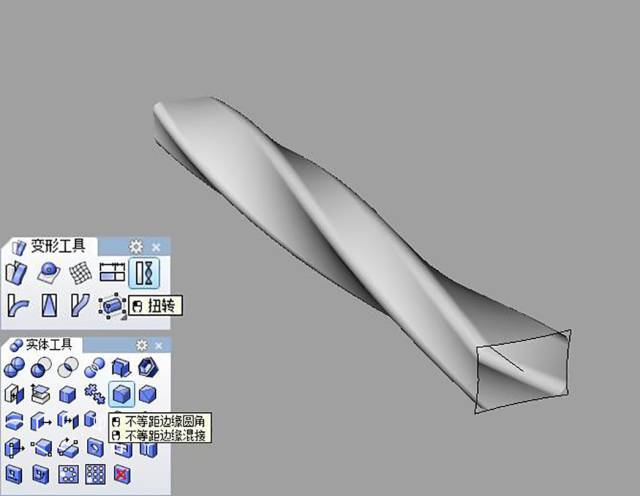
流动曲线,“沿着曲线流动”把直线上的曲面流动到调好形状的曲线上,达到最终效果。注意:选项中延展为“是”。

绘制四条开放曲线,确定苹果把儿的形状。注意:四条曲线的端点需重合。
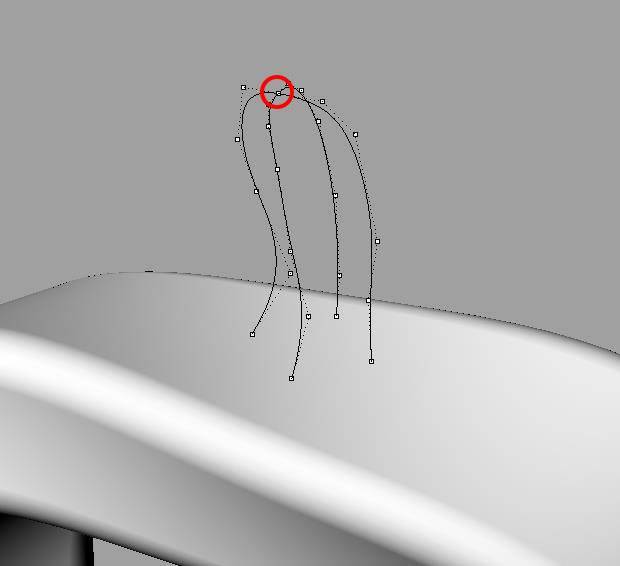
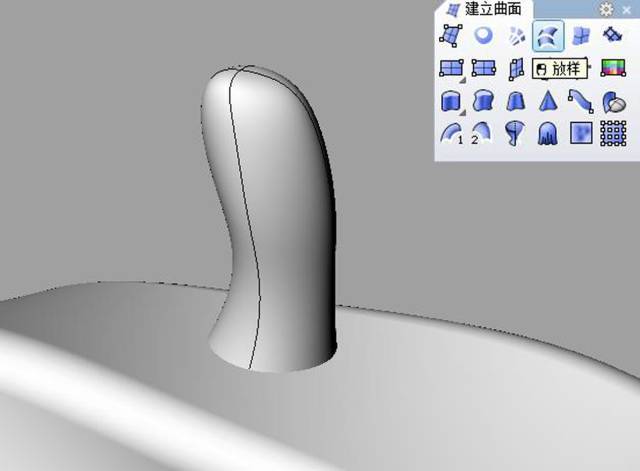
“放样”成面。
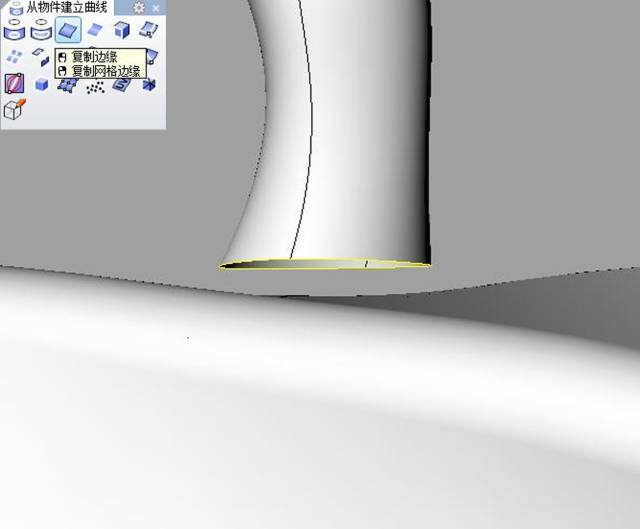
“复制边缘”复制出底边边线。
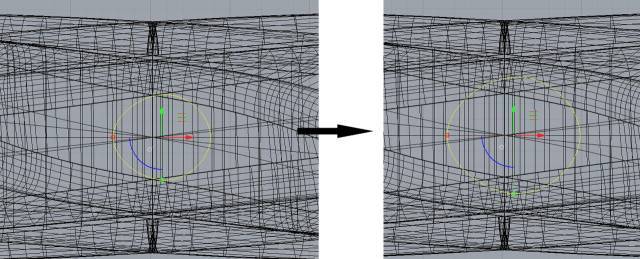
将复制出的曲线等比放大一圈,大小合适即可。
“直线挤出”挤出放大的曲线,并与流动形成的曲面相交。曲面1被曲面2分隔开;然后删掉曲面2和分隔开的公共部分。
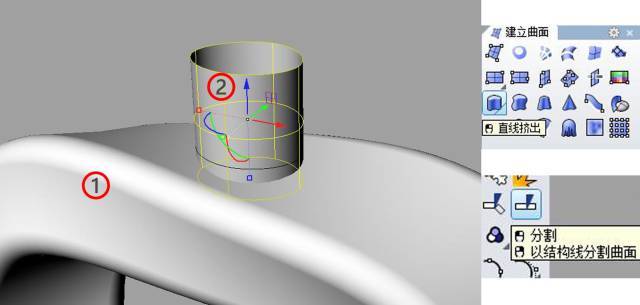
组合完成
“混接曲面”将两个部分用曲面连接起来。全部选中,组合,完成。
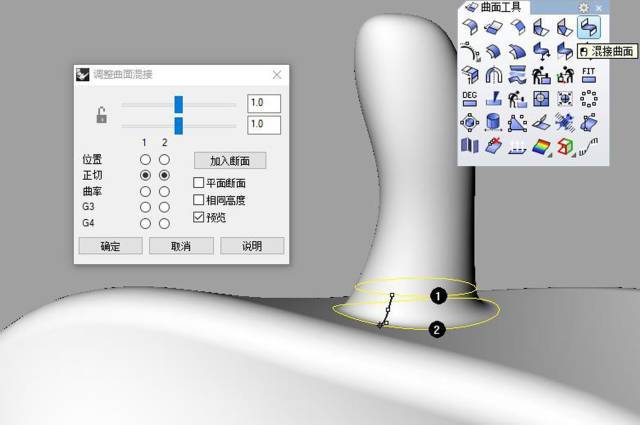
最终组合,完成。
来源:艺术留学申请
相关阅读:
 深圳•南山
深圳•南山

 收藏
收藏